警告
因变量又称被解释变量,自变量又称解释变量
结果解读
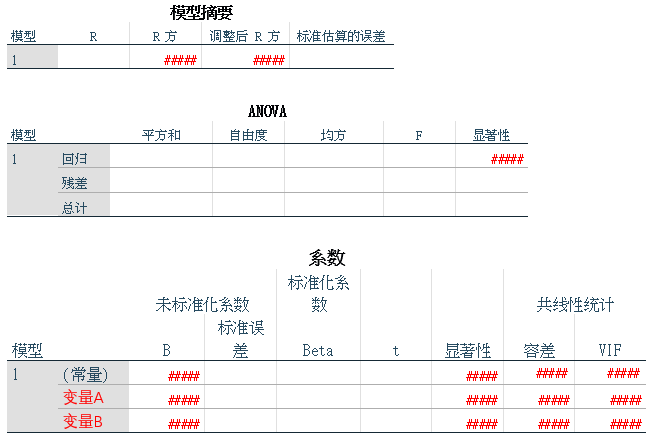
模型摘要
R方和调整后R方越接近1,说明回归方程拟合越优秀。
- 进入策略:调整后R方
- 向后筛选:R方
ANOVA
P < α 时,回归方程整体显著(整体上看,所有自变量与因变量之间的线性关系显著)
系数
- B:回归参数的估计值
- 显著性:回归系数的显著性(自变量与因变量之间的线性关系显著)
- 容差:接近
0,说明共线性强 - VIF:大于
10,说明共线性强
回归变量筛选策略
一、进入(Enter)策略
核心逻辑:强制纳入所有变量,将预先指定的解释变量全部引入回归方程,不进行变量的筛选过程,直接基于所有变量拟合回归模型,后续可结合检验分析变量作用,但初始无筛选动作 。
二、向前筛选(Forward)策略
核心逻辑:变量逐步进入回归方程
- 初始:选与被解释变量线性相关系数最高的变量入方程,做检验。
- 迭代:剩余变量中,找与被解释变量偏相关系数最高且通过检验的变量入方程,重复检验。
- 终止:无新变量可进入方程。
三、向后筛选(Backward)策略
核心逻辑:变量逐步剔除出回归方程
- 初始:所有变量全引入方程,做检验。
- 迭代:在回归系数显著性检验不显著的变量里,剔除t检验值最小的变量,重建方程并检验;若仍有不显著变量,重复剔除。
- 终止:方程中所有变量回归系数检验均显著(或无变量可剔除)。
四、逐步筛选(Stepwise)策略
核心逻辑:向前+向后结合,动态优化变量
- 流程:基于向前筛选引入变量后,额外判断是否需剔除不显著变量,每个引入阶段都可二次优化(剔除冗余)。
- 特点:兼顾“引入显著变量”与“剔除不显著变量”,更灵活精细。