模型法线的Model变换

为什么要进行Model变换

原始的法线向量是模型空间（局部坐标系）的，当我们需要进行光照计算时，便需要将法线向量转换到世界空间，参与与同为世界空间的光照计算（或者处理光照向量）。

错解

• 直接变换：

Normal = vec3(model * vec4(aNormal, 1.0));

这是与位置坐标变换一样的变换方式，补齐 w 分量后应用变换。 但需要注意的是：法线向量只是一个方向向量，不能表达空间中的任何位置，故变换中的位移变换应当忽略。对于法向量，我们只能对它应用缩放和旋转变换。这很简单，只需要将 w 分量设为 0 即可。

• 仅忽略位移变换

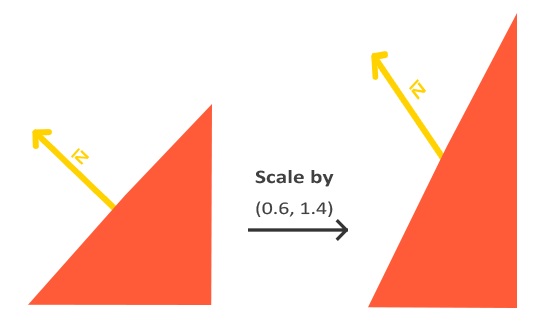
Normal = vec3(model * vec4(aNormal, 0));

虽然vec4(aNormal, 0)中的齐次坐标为0，忽略了位移变换，但果模型矩阵执行了不等比缩放，法向量就不再垂直于表面了。下面的图展示了应用了不等比缩放的矩阵对法向量的影响：

正解

设：局部坐标系内，平面中一条边向量为T，法线向量为N，模型变换矩阵为M，真正的法线变换矩阵为G，求G。 证明： 在局部坐标系内，边与法线垂直，则有$$ \vec{N}\cdot\vec{T}= 0 $$ 将它们都转换到世界坐标系内，$$ (G\vec{N}) \cdot (M\vec{T}) = 0 $$ 点积可以转化为向量乘积的形式，$$ (G\vec{N}) \cdot (M\vec{T}) = (G\vec{N})^\top (M\vec{T}) = 0 $$ 乘积的转置等于各因子转置后的乘积，$$ (G\vec{N})^\top (M\vec{T}) = \vec{N}^\top G^\top M\vec{T} = 0 $$ 根据结合律， $$ \vec{N}^\top G^\top M\vec{T} = \vec{N}^\top（G^\top M）\vec{T} = 0 $$ 又$$ \vec{N}\cdot\vec{T} = 0 \iff \vec{N}^\top\vec{T} = 0 $$ 故得$$ \vec{N}^\top（G^\top M）\vec{T} = \vec{N}^\top\vec{T} $$ 则有 $$ \left\{ \begin{aligned} &\vec{N}^\top（G^\top M）\vec{T} = \vec{N}^\top\vec{T} \\ &\|\vec{N}\| \neq 0 \\ &\|\vec{T}\| \neq 0 \end{aligned} \right. \Rightarrow G^\top M = I \iff G = (M^{-1})^\top $$ 写作代码：

Normal = mat3(transpose(inverse(model) * aNormal;